Распространенным инструментом оценки качества работы менеджеров отдела продаж является аудит качества телефонных звонков, «прослушка».

Предположим, вы задались целью не просто замерить качество телефонных звонков, но зафиксировать рост этого качества. Например, провели обучение (тренинг) менеджеров, либо предложили новую мотивацию за соблюдение стандартов качества, либо что-то еще.

Логично предположить, что рост качества в первом попавшемся, после тренинга, звонке, не будет однозначно свидетельствовать о росте качества в остальных звонках. Скорее всего, и второй удачный звонок тоже однозначно не подтвердит гипотезу, что качество выросло.

Таким образом, речь будет идти о том, что вам придется прослушать если не все, то, по крайней мере, достаточное число звонков после введенных вами изменений, и число звонков, которые необходимо будет прослушать, на самом деле, можно однозначно рассчитать.

Считаем размер выборки

На 15-й странице работы «Планирование размеров выборки для исследований в бихевиоризме» мне попался подходящий пример 2.4 и формула для расчета таких выборок:

В данном примере рассматривается изменение оценки ACT-теста по математике с 24,5 (дисперсия 8,2) до 26,0 баллов при α = 0,05 и мощности = 0,90.

Для удобства работы, я собрал приведенную формулу в Гугл-таблицах:
Калькулятор размера выборки

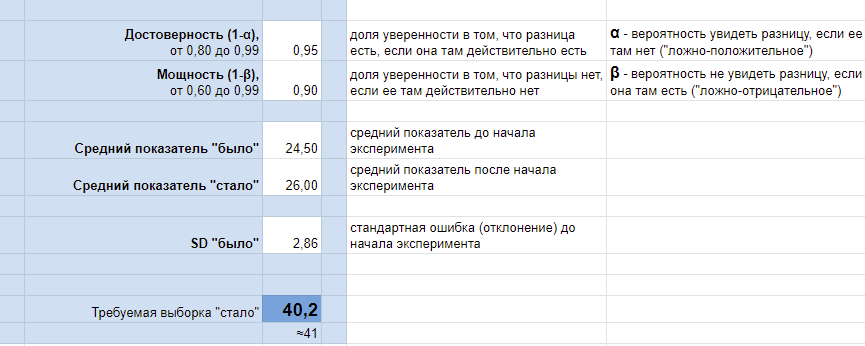
Вам остается скопировать файл, и можете подставлять нужные вам значения. Достоверность разумно выбирать от 80% до 95%, значение мощности — от 60% до 80%. Указываете средний балл оценки звонков до изменений, стандартное отклонение (SD) оценки звонков «до», и ожидаемый средний балл оценки звонков после изменений.

Верификация полученных результатов

Важно понимать, что, даже прослушав требуемое количество звонков «после», все равно необходимо проверять наличие статистически значимых различий через калькулятор А/Б-тестов.

См. также:

https://habr.com/ru/post/339798/
https://people.ucsc.edu/~dgbonett/docs/wrkshp/LectureNotes.pdf

Честно говоря, не знаю, как правильно называется эта штука, но пусть у нее будет рабочее название «скользящее среднее».

Очень часто бывает так, что у нас есть данные с разбивкой по дням. Например, заходы на сайт или звонки в отдел продаж. И, в попытке проанализировать динамику происходящего, мы строим график, получая примерно следующее:

Что здесь не так?

Достаточно очевидно, что, во-первых, график постоянно прыгает вверх-вниз, а, во-вторых, имеет некрасивые экстремумы вроде 16 заявок в октябре или 122 заявок в августе. День на день не приходится, и данные слишком сильно колеблются вокруг среднего значения (кстати, среднее тут равно 63).

А там, где что-то так некрасиво прыгает, часто можно что-то сгладить, используя понятие скользящего среднего.

Скользящее среднее. Простой способ.

Попробуем «сгладить» наш прыгающий график путем расчета среднего числа заявок на дату, исходя из предыдущих 6 дней (7-й — текущий день, итого ровно неделя).

Напротив 07.01.2018 напишем формулу

=СРЗНАЧ(B2:B8)

Протянув формулу по всему году до самой последней строки, получим среднее число заявок на каждую дату за предыдущую неделю. Как будто рамку, шириной в одну неделю, мы двигали по году вдоль с шагом в один день.

Визуально ничего не изменилось. Разве что, раньше были целые значения, а теперь, из-за усреднения, вылезли знаки после запятой — 79,9, 84,1. Обновим наш график:

На месте прежнего, «прыгающего», графика, теперь более гладкая линия. Исчезли аномальные дни с 16 и 122 звонками в октябре и в августе, зато теперь, на «недельном» масштабе, стал заметнее провал на майские праздники.

Скользящее среднее. Сложный способ.

Некоторое время попрактиковавшись с вычислением скользящего среднего, вы обратите внимание, что, чем шире вы будете брать «окно» для расчета среднего на дату, тем сильнее будет сглаживаться ваш график. Теоретически, вы можете взять окно шириной в 365 дней... и получится практически ровная линия. А при окне шириной в 1 день — график не сглаживается вообще.

В этот момент становится понятно, что «7 дней» из первого примера — это просто случайное число, а на самом деле, оно может быть абсолютно любым — все зависит лишь от ваших предпочтений и представлений о том, что вы хотите увидеть и проанализировать.

Попробуем не задавать жестко ширину нашего «окна», а сделать его параметром нашего графика. Пусть «окно» в 7 дней, используемое для сглаживания графика, будет зависеть от цифры «7», помещенной в ячейку C1. И пусть, если мы меняем «7» на «5» или «30», Эксель перестраивает наш график.

Итак, настало время для красивой формулы в ячейке C8:

=СРЗНАЧЕСЛИМН(B$2:B$365;A$2:A$365;"<="&A8;A$2:A$365;">="&(A8-$C$1+1))

Функция

=СРЗНАЧЕСЛИМН()

берет и считает среднее значение для тех дат, для которых будут выполняться оба условия:

1. Дата, которая участвует в расчете среднего, должна быть больше или равна дате, отстоящей от даты, для которой мы рассчитываем среднее, назад на N-1 дней (где N — ширина нашего «окна»).
2. Дата, которая участвует в расчете среднего, должна быть меньше или равна дате, для которой мы это среднее рассчитываем.

Проще говоря, для расчета среднего числа заявок на 18 апреля при N=7 дней, мы возьмем среднее от числа заявок с 12 по 18 апреля (больше или равно 12 апреля и меньше или равно 18 апреля). Для расчета среднего числа заявок на 19 апреля — среднее от числа заявок с 13 по 19 апреля, и так далее.

Выделим ячейку C1 под наш параметр N, тогда формула для 07.01.2018 выглядит так:

=СРЗНАЧЕСЛИМН(B$2:B$365;A$2:A$365;"<="&A8;A$2:A$365;">="&(A8-$C$1+1))

Итого, теперь мы имеем уже знакомый нам «сглаженный» 7-дневный график, но ширину «окна» задали не строго, а привязали ее к параметру, записанному в ячейке C1:

Меняя значение параметра в ячейке C1, получаем все более и более ровную линию. Вот, для сравнения, наложенные друг на друга графики при N=1, N=5, N=30: